保険業界でアクチュアリーとして働いていた筆者が、生命保険の保険料がどのような要素で構成されているのか、またどのように計算されているのかを簡単な数値例を使いながらわかりやすく解説していきます。
今回は初回(前々回)の応用です。初回は計算を簡単にするために毎年の死亡者数が一定の状況を考えました。今回は少し計算が複雑になりますが、毎年の死亡率が一定の状況を考えていきましょう。
初回(前々回)のおさらい
シリーズ化している『世界一わかりやすい保険料の計算方法』ですが、前回は保険料に対する利回りの影響を考えました。今回は死亡率についてより深く考えるために、利回りをゼロに戻して死亡率の影響だけを見ていくことにします。このため、実質的にはこの記事は初回(前々回)の続きの内容になりますので、まだ初回の記事のお読みになっていない方はこちらも是非読んでみてください。
~計算の準備~
まず、初めに計算の準備として死亡率の考え方について整理しておきます。
死亡率とは本来年始の人数にかけて死亡者数を計算するためのものです。その年に亡くなった人の人数を年始の人口で割って求める、といった方が正確かもしれません。
しかし初回と前回の計算では死亡率を最初の人数に対して2%としました。これは初回の脚注でも触れていますが、人数の計算が必要以上に複雑になることを避けるためです。
死亡者数を一定とすることで死亡者数は毎年2人(最初の人数は100人)とすることができ、人数をイメージしやすくすることができました。しかし、繰り返しになりますが、本来1年間の死亡率とは特段の断りがない限り年始の人数にかかるものです。
このため今回は、死亡率が毎年2%で一定の場合、死亡者数が一定の場合と保険料に対してどういった影響が出てくるかを考えていきましょう。
保険料の計算例①:保険期間1年の死亡定期保険
今回は死亡率について理解を深めるために、死亡率を各年始の2%としますが、それ以外の条件は初回と全く同じにします。つまり、保険金額を100万円とし、保険金額比例の事業費率を保険金額の1%と保険料比例事業費率を保険料の3%とします。
この場合の保険期間1年の死亡定期保険の年払保険料はいくらになるでしょうか?実はこれは初回に考えた保険料と同額になります。最初の人数を100人とすると、死亡者数を毎年2人としても死亡率を毎年2%としても最初の年だけは死亡者数は2人で変わりません。ですので、保険料の計算式は以下のとおり全く同じになります。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ \underset{\scriptsize\mbox{保険料収入}}{\underline{\mbox{保険料}}} = \underset{\scriptsize\mbox{保険金支払}}{\underline{\mbox{100万円}\times 2\%}} + \underset{\scriptsize\mbox{保険金額比例の事業費}}{\underline{\mbox{100万円}\times 1\%}} + \underset{\scriptsize\mbox{保険料比例の事業費}}{\underline{\mbox{保険料}\times 3\%}} }} \end{align*} $$
保険料を移行してまとめて計算すると、30,928円と求まるかと思います。保険料の内訳については初回の記事と同じですので割愛します。もし説明が不足していると感じられた場合は、上のリンクから初回の記事をご確認ください。問題ない方はすぐに次の保険期間を2年にした例に進みましょう。
保険料の計算例②:保険期間2年の死亡定期保険
今回の記事はここからが本番です。保険期間の2年目から死亡率を一定とした影響が出てきます。ここでも結局小数は消えてくれないのですが、例え小数であったとしても人数の方がイメージしやすいと思いますので、最初の人数を100人として計算しましょう。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ \underset{\scriptsize\mbox{1年目の保険料収入}}{\underline{\mbox{保険料}\times 100人}} + \underset{\scriptsize\mbox{2年目の保険料収入}}{\underline{\mbox{保険料}\times 98人}} = \underset{\scriptsize\mbox{1年目の保険金支払}}{\underline{\mbox{100万円}\times 2}} + \underset{\scriptsize\mbox{2年目の保険金支払}}{\underline{\mbox{100万円}\times 98人\times 2%}} + \underset{\scriptsize\mbox{保険金額比例の事業費}}{\underline{\mbox{100万円}\times 1}} + \underset{\scriptsize\mbox{保険料比例の事業費}}{\underline{\mbox{保険料}\times 198 \times 3\%}} }} \end{align*} $$
ポイントとなるのは2年目の保険金支払の部分です。今回の例では死亡率を年間2%としていますので、2年目の死亡者数は年始に生存している98に対しての2%として計算する必要があります。
このため、2年目の死亡者数は98×2%で1.96人になります。人数が小数なのは違和感がありますが、期待値の話をしていますのでこういう結果もあり得るわけです。
さて、この方程式を保険料で解いて25,825円になったでしょうか?計算例①と同様に保険料の内訳を計算しますと以下のとおりになります。例えば保険料収入の合計の部分は四捨五入する前の保険料(26,033.53・・・円)に1.98をかけてから四捨五入して金額に直しています。
| 収入/支出 | 項目 | 金額(死亡者数一定) | 金額(死亡率一定) |
|---|---|---|---|
| 収入 | 保険料収入の合計 | 51,546円 | 51,534円 |
| 支出 | 保険金支払の合計 | 40,000円 | 39,600円 |
| 支出 | 保険金比例の事業費 | 10,000円 | 10,000円 |
| 支出 | 保険料比例の事業費 | 1,546円 | 1,534円 |
保険料の計算例③:保険期間10年の死亡定期保険
最後に保険期間が10年の場合の保険料を考えてみましょう。保険料の払込期間も同じ10年とします。まず左辺の保険料ですが、以下のような計算式になります。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料 = \underset{\scriptsize\mbox{1年目の保険料収入}}{\underline{\mbox{保険料}\times 100人}} + \underset{\scriptsize\mbox{2年目の保険料収入}}{\underline{\mbox{保険料}\times 98人}} + \underset{\scriptsize\mbox{3~8年目の保険料収入}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{9年目の保険料収入}}{\underline{\mbox{保険料}\times 85.05人}} + \underset{\scriptsize\mbox{10年目の保険料収入}}{\underline{\mbox{保険料}\times 83.37人}} }} \end{align*} $$
初回で取り扱った最初の人数が100人で毎年死亡者数が2人の場合に比べ、死亡者数が少なくなるため生存者は多くなります。保険料は生存者から集めるため、保険料を集めることができる人数が増えていることがわかります(9年目、10年目は初回、前回とそれぞれ84人及び82人でした)。
死亡率が2%であるため、生存率は98%になりますから、毎年年始の人数に98%をかけて翌年始の人数を求めることになります。また上の計算式を前回と同様に、経過年数をtと置けば以下のような和の形でも表すことができます。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料 = \mbox{保険料} \sum_{t=0}^{9}\mbox{100×(1-2%)}^t }} \end{align*} $$
続いて、右辺の1つ目の要素である保険金支払について考えてみます。今回の例では最初の人数ではなく各年始の人数に死亡率がかかるため、死亡者数は常に2人より少なくなります。
具体的な人数は以下の算式に含まれています。例えば2年目の死亡者数は100人×98%×2%で求められています。98%は1年目の1年間の生存率です。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 保険金支払 = \underset{\scriptsize\mbox{1年目の保険金支払}}{\underline{\mbox{100万円}\times 2人}} + \underset{\scriptsize\mbox{2年目の保険金支払}}{\underline{\mbox{100万円}\times 1.96人}} + \underset{\scriptsize\mbox{3~8年目の保険金支払}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{9年目の保険金支払}}{\underline{\mbox{100万円}\times 1.70人}} + \underset{\scriptsize\mbox{10年目の保険金支払}}{\underline{\mbox{100万円}\times 1.67人}} }} \end{align*} $$
保険料収入の計算式と同様に経過年数をtとおくことで、この計算式も和の形で表現することができます。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 支払保険金 = 100万円 × \sum_{t=0}^{9}\mbox{100×(1-2%)}^t×\mbox{2%} }} \end{align*} $$
最後に右辺の2つ目の要素である事業費支出について考えてみましょう。
保険金比例の事業費の支出は新契約費のイメージですので最初だけかかります。
保険料比例の事業費は集金費のイメージですので保険料を集めるタイミング、つまり年始の人数に対してかかることになります。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 事業費支出 = \underset{\scriptsize\mbox{保険金比例の事業費}}{\underline{\mbox{100万円 × 100人 × 1%}}} + \underset{\scriptsize\mbox{1年目の保険料比例の事業費}}{\underline{\mbox{保険料 × 100人 × 3%}}} + \underset{\scriptsize\mbox{2年目の保険料比例の事業費}}{\underline{\mbox{保険料 × 98人 × 3%}}} + \underset{\scriptsize\mbox{3~8年目の保険料比例の事業費}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{9年目の保険料比例の事業費}}{\underline{\mbox{保険料 × 85.05人 × 3%}}} + \underset{\scriptsize\mbox{10年目の保険料比例の事業費}}{\underline{\mbox{保険料 × 83.37人 × 3%}}} }} \end{align*} $$
事業費支出はも同様に和の形で表すと以下のような計算式になりますね。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 事業費支出 = \mbox{100万円 × 100人 × 1%} + \mbox{保険料 × 3% × } \sum_{t=0}^{9}\mbox{100×(1-2%)}^t }} \end{align*} $$
この計算式を保険料について解くと、保険料は21,746円と求めることができます。保険料の内訳は以下のとおりとなります。
例えば保険料収入の合計は、上の計算式に21,746円を代入して100で割ることで求めています。上の計算式は人数に直すために100倍しましたので1人分の保険料を求めるために100で割って1人分に戻しています。
| 収入/支出 | 項目 | 金額(死亡者数一定) | 金額(死亡率一定) |
|---|---|---|---|
| 収入 | 保険料収入の合計 | 216,495円 | 198,894円 |
| 支出 | 保険金支払の合計 | 200,000円 | 182,927円 |
| 支出 | 保険金比例の事業費 | 10,000円 | 10,000円 |
| 支出 | 保険料比例の事業費 | 6,495円 | 5,967円 |
(参考)保険期間が3年から9年の場合
ご参考までに保険期間が1年から10年まで、上記の前提で保険料の計算とその内訳を計算したものを表にしてみました。エクセルなどでも簡単に再現できるかと思いますので、ご興味のある方は是非再計算してみてください!
| 保険期間 | ① 年払保険料 | ② 保険料の合計 | ③ 保険金の合計 | ④ 保険金比例事業費の合計 | ⑤ 保険料比例事業費の合計 | ⑥ 支出(③+④+⑤) | chk ②=⑥ |
|---|---|---|---|---|---|---|---|
| 1 | 30,928 | 30,928 | 20,000 | 10,000 | 928 | 30,928 | TRUE |
| 2 | 25,825 | 51,134 | 39,600 | 10,000 | 1,534 | 51,134 | TRUE |
| 3 | 24,125 | 70,936 | 58,808 | 10,000 | 2,128 | 70,936 | TRUE |
| 4 | 23,274 | 90,342 | 77,632 | 10,000 | 2,710 | 90,342 | TRUE |
| 5 | 22,765 | 109,360 | 96,079 | 10,000 | 3,281 | 109,360 | TRUE |
| 6 | 22,425 | 127,998 | 114,158 | 10,000 | 3,840 | 127,998 | TRUE |
| 7 | 22,182 | 146,262 | 131,874 | 10,000 | 4,388 | 146,262 | TRUE |
| 8 | 22,000 | 164,162 | 149,237 | 10,000 | 4,925 | 164,162 | TRUE |
| 9 | 21,859 | 181,703 | 166,252 | 10,000 | 5,451 | 181,703 | TRUE |
| 10 | 21,746 | 198,894 | 182,927 | 10,000 | 5,967 | 198,894 | TRUE |
また、保険期間ごとに「①年払保険料」の金額もグラフにしてみました。
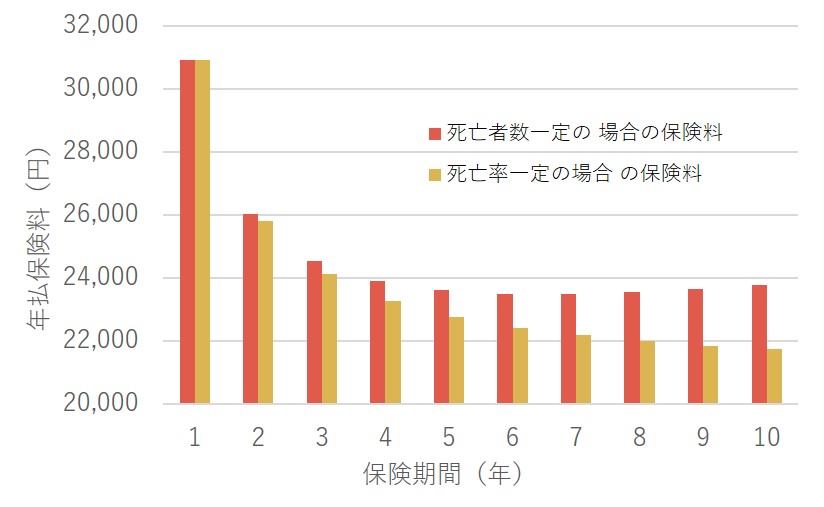
また、保険期間ごとに「①年払保険料」の金額もグラフにしてみました。グラフだけですとどれくらい保険料が割り引かれたかが正確に読み取れませんので、以下の表も合わせてご覧ください。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 死亡者数一定の 場合の保険料 | 30,928 | 26,034 | 24,546 | 23,913 | 23,625 | 23,512 | 23,501 | 23,556 | 23,657 | 23,791 |
| 死亡率一定の場合 の保険料 | 30,928 | 25,825 | 24,125 | 23,274 | 22,765 | 22,425 | 22,182 | 22,000 | 21,859 | 21,746 |
| 保険料の割引 | 0.0% | 0.8% | 1.7% | 2.7% | 3.6% | 4.6% | 5.6% | 6.6% | 7.6% | 8.6% |
保険期間が長くなるつれて割引効果が大きいことがわかりました。ただ、これは割引というよりは単に死亡率の水準が異なるから保険料が安くなっているだけです。保険料は当然予想される死亡率が高ければ高くなります。
最初の人数が100人で死亡者数が毎年2人で一定とは年始に対する死亡率に直すと毎年何%になるのでしょうか?例えば2年目の場合は98人中2人亡くなるということですので2÷98×100で約2.04%です。
3年目は年始の人数が約96.04人ですから死亡率は2÷98×100で2.08%となります。年を追うごとに年始の人数は死亡者数の分減っていきますので、その中で死亡者数が一定であれば当然にどんどん高くなっていきます。このため最初の人数が100人で死亡人数が2人で一定の場合の死亡率は小数第2位まで求めると以下の表のような数字になります。
| 経過年数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 死亡率 | 2.00% | 2.04% | 2.08% | 2.13% | 2.17% | 2.22% | 2.27% | 2.33% | 2.38% | 2.44% |
この機会に死亡者数が同じであることと死亡率が同じであるとは同じではないことを覚えておくと良いと思います。なお、実際の死亡率は通常年齢が上がるとともに上がっていきますので、死亡率が一定であるという仮定よりは現実的なのかもしれませんね。
まとめ
今回の記事では「【定期保険篇】世界一わかりやすい保険料の計算方法 ー その③」と題して、死亡定期保険の保険料について死亡率が一定の場合の計算方法を解説していきました。
次は「世界一わかりやすい保険料の計算方法③」と題して、前回取り扱った利回りと今回取り扱った死亡率の2つを同時に考えた場合の計算方法を見ていきます。
ご興味があればぜひこちらの記事もご覧ください。
それではまたお会いできることを楽しみにしています。
【参考文献】
アクチュアリー試験、1次試験指定テキスト:二見隆著、生命保険数学<上巻>及び<下巻>
アクチュアリー試験、2次試験指定テキスト:保険1(生命保険)及び保険2(生命保険)






コメント