保険業界でアクチュアリーとして働いていた筆者が、生命保険の保険料がどのような要素で構成されているのか、またどのように計算されているのかを簡単な数値例を使いながらわかりやすく解説していきます。
今回は前回の応用で保険料の計算において利回りの影響を考慮していきます。
前回のおさらい
前回扱った世界一わかりやすい保険料の計算方法が好評でしたので、もう少し深く知りたいという方向けにこちらをシリーズ化することに致しました。前回の内容についてはこちらをご参照ください。
さて、前回は利回りをゼロとして保険料を計算してみましたが、今回は利回りを考慮した保険料の計算例について見ていきます。保険料の計算に使われる利回りは業界の用語で「予定利率」と呼ばれますが、この記事ではできるだけ業界特有の表現は避け、単に利回りと呼ぶことにします。
前回の記事の冒頭ですべての保険料は以下の算式によって計算されると解説しました。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 保険料収入の現在価値 = 保険金支払の現在価値 + 事業費の現在価値 }} \end{align*} $$
現在価値という考え方が本当にわかりにくいのですが、今回はこの部分を詳しく解説して保険料の計算にまで繋げていきたいと思います。
~計算の準備~
まず前提として、保険会社は集めた保険料のほとんどを債券や株式などで運用しています。保険の商品を作るときに、債券や株式で最低でも年間5%の利回りで運用できそうだとすると、保険料を計算するときに、集めた保険料を毎年5%で運用できるものとして計算します。
最近の超低金利の状況ではありえない水準ですが、5%という数字は簡単ですので、今回はこの数字を使って前回の計算をやり直してみましょう。
ただ、実際に計算を行う前に現在価値の考えを整理しておくことが大切です。
利回りの影響を計算式に入れるためには知っておかなくてはならないことがあります。それは経過した時間によって1円の価値が変わってしまうことです。
1年目の保険料と2年目の保険料がともに1,000円だった場合、以下のという等式は正しいでしょうか?
$$ \begin{align*} {\color{black}{ 『1年目の1,000円の保険料=2年目の1,000円の保険料』 }} \end{align*} $$
答えはNoです。なぜなら1年目の保険料の1,000円は1年間5%で運用できるため、2年目には1,050円になっているはずだからです。
つまり、異なるタイミングで集めるお金や支払うお金の価値をイコールで繋いだ計算式で表現するためには、どこかのタイミングに揃えてあげないといけません。
この時に「今現在」に揃えようという考え方が現在価値であり、保険料計算における「現在」とは契約時点のことを指します。上の1,000円の例だと2年目の1,000円を1+5% = 1.05で割って、952円と考えるということが現在価値への直し方になります。
前置きが長くなりましたが、すべてのお金(保険料の収入、保険金の支払、事業費支出)は契約時点の価値で考える、ということはご理解頂けたのではないかと思います。
さて、これで利回りを考慮した保険料の計算の準備が整ったのですが、実際の計算に当たってはもう1つ前提が必要になります。
それは収入や支出のタイミングです。2年目の保険料の現在価値と言っても、保険料を集めるタイミングが年始なのか年末なのか、それとも年の中央なのかによってどれくらいの期間調整すれば良いのかがわかりません。
例えば2年目の保険料を年始に集める場合は1.05で1回割れば良いですが、年末に集める場合は1.05で2回割らないといけません。このため、今回の例では収入と事業費の支出は年始に、保険金の支払いは年末に行われるとします。
さて、ようやく計算の準備が整いました。保険料の具体的な計算に進んでいきましょう。
保険料の計算例①:保険期間1年の死亡定期保険
今回は利回りについて理解を深めるために利回りを5%としますが、それ以外の条件は前回と全く同じにします。つまり、保険金額を100万円で1年間のある人の死亡率を(最初の人数の)2%、保険金額比例の事業費率を保険金額の1%と保険料比例事業費率を保険料の3%とします。
続いて収入と支出のタイミングは以下の図のとおりです。
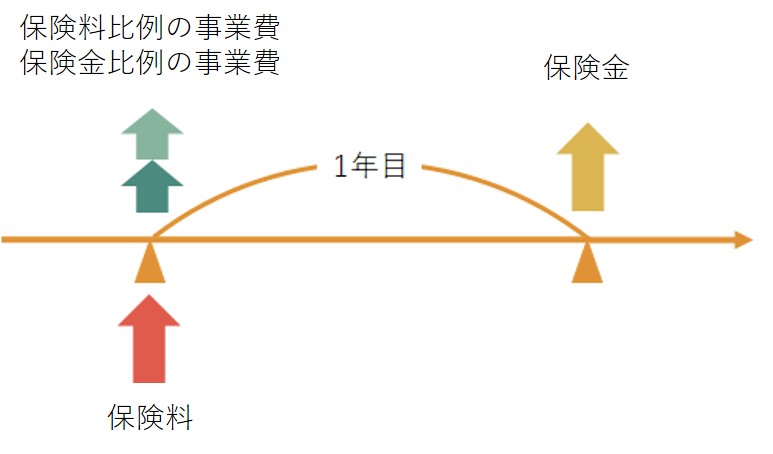
この図を見ますとタイミングがずれているのは保険金だけですね。ということは保険金額だけ現在価値に戻す必要がありそうです。これらの点に気を付けて計算式を立てますと以下のとおりとなります。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ \underset{\scriptsize\mbox{保険料収入}}{\underline{\mbox{保険料}}} = \underset{\scriptsize\mbox{保険金支払}}{\underline{\mbox{100万円 × 2% ÷ 1.05}}} + \underset{\scriptsize\mbox{保険金額比例の事業費}}{\underline{\mbox{100万円}\times 1\%}} + \underset{\scriptsize\mbox{保険料比例の事業費}}{\underline{\mbox{保険料}\times 3\%}} }} \end{align*} $$
この計算式を保険料について解くと、保険料は29,946円と求めることができます。保険料の内訳は以下のとおりとなります。
支出の合計金額が保険料の収入金額でぴったり賄えていることを確認してみてください。なお、参考として前回求めた利回りゼロの場合の金額も残しています。今回求めた金額が一番右の列です。
| 収入/支出 | 項目 | 金額(利回りゼロ) | 金額(利回り5%) |
|---|---|---|---|
| 収入 | 保険料収入の合計 | 30,928円 | 29,946円 |
| 支出 | 保険金支払の合計 | 20,000円 | 19,048円 |
| 支出 | 保険金比例の事業費 | 10,000円 | 10,000円 |
| 支出 | 保険料比例の事業費 | 928円 | 898円 |
保険料を比較すると前回計算した金額のおよそ96.8%と3.2%程度安くなっています。保険金支払は現在価値に直した分安くなりましたが、その他の事業費は変わりませんでしたので、結果として利回りの5%ほどは安くなりませんでした。利回りの保険料に対する感応度が見れて面白いですね。
保険料の計算例②:保険期間2年の死亡定期保険
次に保険期間が2年の場合を考えてみましょう。保険金額などは上の例と同じですので、収入と支出のタイミングについて整理する必要があります。
保険金比例の事業費は新契約に関係する経費のイメージですので契約時点だけ、保険料比例の事業費は集金費のイメージですので保険料と同じタイミングに発生することになります。
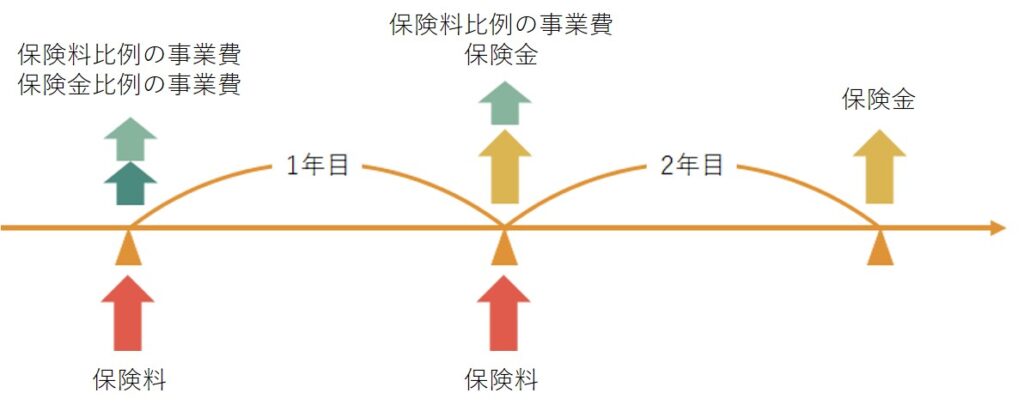
この前提のもとまずは計算式の左辺を考えてみましょう。左辺は保険料収入の現在価値を表しますので以下のとおりになります。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料の現在価値 = \underset{\scriptsize\mbox{1年目の保険料収入}}{\underline{\mbox{100万円 × 100人}}} + \underset{\scriptsize\mbox{2年目の保険料収入}}{\underline{\mbox{100万円 × 98人 ÷ 1.05}}} }} \end{align*} $$
次に計算式の右辺を考えてみましょう。右辺は支出の現在価値を表しますが、保険金の支払いと事業費の支出がありますので、まずは保険金の支払いについて考えてみます。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料の現在価値 = \underset{\scriptsize\mbox{1年目の保険金支払}}{\underline{\mbox{100万円 × 2人 ÷ 1.05}}} + \underset{\scriptsize\mbox{2年目の保険金支払}}{\underline{\mbox{100万円 × 2人 ÷ 1.05 ÷ 1.05}}} }} \end{align*} $$
最後に事業費の支出について考えてみましょう。読者の皆さんも一緒に考えてみてください。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 事業費支出の現在価値 = \underset{\scriptsize\mbox{保険金比例の事業費}}{\underline{\mbox{100万円 × 1}}} + \underset{\scriptsize\mbox{1年目の保険料比例の事業費}}{\underline{\mbox{100万円 × 100人 × 3%}}} + \underset{\scriptsize\mbox{2年目の保険料比例の事業費}}{\underline{\mbox{100万円 × 98人 × 3% ÷ 1.05}}} }} \end{align*} $$
上記のような計算式になりましたでしょうか?これで収入と支出の項がすべて準備できましたね。これらの3つの計算式をまとめると以下のとおりになります。小数第3位を四捨五入して小数第2位まで表示しています。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ \underset{\scriptsize\mbox{2年分の保険料収入}}{\underline{\mbox{保険料}\times 193.33}} = \underset{\scriptsize\mbox{2年分の保険金支払}}{\underline{\mbox{100万円}\times 3.72}} + \underset{\scriptsize\mbox{保険金額比例の事業費}}{\underline{\mbox{100万円}\times 1}} + \underset{\scriptsize\mbox{2年分の保険料比例の事業費}}{\underline{\mbox{保険料}\times 193.33 \times 3\%}} }} \end{align*} $$
この計算式を保険料について解くと、保険料は25,163円と求めることができます。保険料の内訳は以下のとおりとなります。例えば保険料収入の合計は以下のように求めています。
$$ \begin{align*} {\color{black}{25,163円 × (1 + 0.98 ÷ 1.05) = 48,648円}} \end{align*} $$
| 収入/支出 | 項目 | 金額(利回りゼロ) | 金額(利回り5%) |
|---|---|---|---|
| 収入 | 保険料収入の合計 | 51,546円 | 48,648円 |
| 支出 | 保険金支払の合計 | 40,000円 | 37,188円 |
| 支出 | 保険金比例の事業費 | 10,000円 | 10,000円 |
| 支出 | 保険料比例の事業費 | 1,546円 | 1,459円 |
保険料の計算例③:保険期間10年の死亡定期保険
最後に保険期間が10年の場合の保険料を考えてみましょう。保険料の払込期間も同じ10年とします。まず左辺の保険料ですが、以下のような計算式になります。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料 = \underset{\scriptsize\mbox{1年目の保険料収入}}{\underline{\mbox{保険料}\times 100人}} + \underset{\scriptsize\mbox{2年目の保険料収入}}{\underline{\mbox{保険料}\times 98人 \div 1.05}} + \underset{\scriptsize\mbox{3~8年目の保険料収入}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{9年目の保険料収入}}{\underline{\mbox{保険料}\times 84人 \div 1.05^8}} + \underset{\scriptsize\mbox{10年目の保険料収入}}{\underline{\mbox{保険料}\times 82人 \div 1.05^9}} }} \end{align*} $$
複雑に見えますが、ひとつひとつ丁寧に見ていきますと、保険期間が2年の例と同じであることに気がつくかと思います。経過年数をtと置けば以下のような和の形でも表すことができます。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料 = 保険料× \sum_{t=0}^{9}\frac{100-2t}{1.05^t} }} \end{align*} $$
続いて、右辺の1つ目の要素である保険金支払について考えてみます。保険金は年末に支払われますので、1年目の保険金支払から1.05で割って現在価値に直す必要があります。
また、最後の10年目の保険金支払は10年間で1.05の10乗で割る必要があります。2~9年目はこの間になりますので、求める計算式は以下のとおりになります。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 保険金支払 = \underset{\scriptsize\mbox{1年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05}} + \underset{\scriptsize\mbox{2年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05^2}} + \underset{\scriptsize\mbox{3~8年目の保険金支払}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{9年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05^9}} + \underset{\scriptsize\mbox{10年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05^{10}}} }} \end{align*} $$
保険料収入の計算式と同様に経過年数をtとおくことで、この計算式も和の形で表現することができます。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 支払保険金 = 100万円 × 2人 \sum_{t=0}^{9}\frac{1}{1.05^{t+1}} }} \end{align*} $$
最後に右辺の2つ目の要素である事業費支出について考えてみましょう。
保険金比例の事業費は1年目の年始のみの支出のため1.05で割る必要はありません。
保険料比例の事業費は保険料収入の例で既に見たとおり2回目以降毎年1.05ずつの割引がかかってきますね。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 事業費支出 = \underset{\scriptsize\mbox{保険金比例の事業費}}{\underline{\mbox{100万円 × 100人 × 1%}}} + \underset{\scriptsize\mbox{1年目の保険料比例の事業費}}{\underline{\mbox{保険料 × 100人 × 3%}}} + \underset{\scriptsize\mbox{2年目の保険料比例の事業費}}{\underline{\mbox{保険料 × 98人 × 3%} \div 1.05}} + \underset{\scriptsize\mbox{3~8年目の保険料比例の事業費}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{9年目の保険料比例の事業費}}{\underline{\mbox{保険料 × 84人 × 3%} \div 1.05^8}} + \underset{\scriptsize\mbox{10年目の保険料比例の事業費}}{\underline{\mbox{保険料 × 82人 × 3%} \div 1.05^9}} }} \end{align*} $$
事業費支出は特に保険料比例の部分については保険料収入と同じまとめ方ができます。まとめると以下のような形で表すことができますね。
$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 事業費支出 = {\mbox{100万円 × 100人 × 1%} + \mbox{保険料 × 3%} \sum_{t=0}^{9}\frac{100-2t}{1.05^t}} }} \end{align*} $$
この計算式を保険料について解くと、保険料は22,775円と求めることができます。保険料の内訳は以下のとおりとなります。
例えば保険料収入の合計は、上の計算式に22,775円を代入して100で割ることで求めています。上の計算式は人数に直すために100倍しましたので1人分の保険料を求めるために100で割って1人分に戻しています。
| 収入/支出 | 項目 | 金額(利回りゼロ) | 金額(利回り5%) |
|---|---|---|---|
| 収入 | 保険料収入の合計 | 216,495円 | 169,520円 |
| 支出 | 保険金支払の合計 | 200,000円 | 154,435円 |
| 支出 | 保険金比例の事業費 | 10,000円 | 10,000円 |
| 支出 | 保険料比例の事業費 | 6,495円 | 5,086円 |
(参考)保険期間が3年から9年の場合
ご参考までに保険期間が1年から10年まで、上記の前提で保険料の計算とその内訳を計算したものを表にしてみました。エクセルなどでも再現できるかと思いますので、ご興味のある方は是非再計算してみてください!
| 保険期間 | ① 年払保険料 | ② 保険料の合計 | ③ 保険金の合計 | ④ 保険金比例事業費の合計 | ⑤ 保険料比例事業費の合計 | ⑥ 支出(③+④+⑤) | chk ②=⑥ |
|---|---|---|---|---|---|---|---|
| 1 | 29,946 | 29,946 | 19,048 | 10,000 | 898 | 29,946 | TRUE |
| 2 | 25,163 | 48,648 | 37,188 | 10,000 | 1,459 | 48,648 | TRUE |
| 3 | 23,701 | 66,459 | 54,465 | 10,000 | 1,994 | 66,459 | TRUE |
| 4 | 23,070 | 83,422 | 70,919 | 10,000 | 2,503 | 83,422 | TRUE |
| 5 | 22,771 | 99,577 | 86,590 | 10,000 | 2,987 | 99,577 | TRUE |
| 6 | 22,639 | 114,963 | 101,514 | 10,000 | 3,449 | 114,963 | TRUE |
| 7 | 22,602 | 129,616 | 115,727 | 10,000 | 3,888 | 129,616 | TRUE |
| 8 | 22,624 | 143,571 | 129,264 | 10,000 | 4,307 | 143,571 | TRUE |
| 9 | 22,686 | 156,862 | 142,156 | 10,000 | 4,706 | 156,862 | TRUE |
| 10 | 22,775 | 169,520 | 154,435 | 10,000 | 5,086 | 169,520 | TRUE |
また、保険期間ごとに「①年払保険料」の金額もグラフにしてみました。
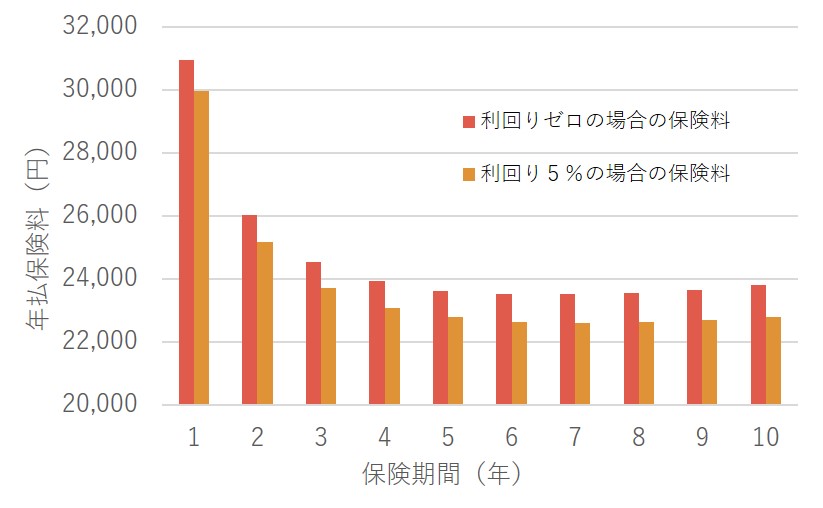
また、保険期間ごとに「①年払保険料」の金額もグラフにしてみました。グラフだけですとどれくらい保険料が割り引かれたかが正確に読み取れませんので、以下の表も合わせてご覧ください。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 利回りゼロの 場合の保険料 | 30,928 | 26,034 | 24,546 | 23,913 | 23,625 | 23,512 | 23,501 | 23,556 | 23,657 | 23,791 |
| 利回り5%の 場合の保険料 | 29,946 | 25,163 | 23,701 | 23,070 | 22,771 | 22,639 | 22,602 | 22,624 | 22,686 | 22,775 |
| 保険料の割引 | 3.2% | 3.3% | 3.4% | 3.5% | 3.6% | 3.7% | 3.8% | 4.0% | 4.1% | 4.3% |
保険期間が長くなるつれて割引効果が大きいことがわかりました。これは今回の例では保険金の支払金額が毎年一定金額であるのに対し、保険料の収入金額は毎年減っていくためです。
保険料は経過が浅い年にたくさん集めるため、その分たくさん運用できて保険料を安くすることができる、と考えても良いでしょう。
まとめ
今回の記事では、「【定期保険篇】世界一わかりやすい保険料の計算方法 ー その②」と題して、前回の応用として利回りを考慮した保険料の計算について考えてみました。特に現在価値とは『異なるタイミングで集めるお金や支払うお金は、すべて利回りを考慮して契約時点に戻す』という考え方でした。今後も度々出てくる考え方ですので、忘れてしまったら是非このページに戻ってきてください。
さて、次の記事では、また利回りをゼロに戻したうえで、今度は死亡率についてより現実的な前提を用いて計算します。
更に、利回りと死亡率について現実に近い前提で計算した例については以下の記事で取り扱っています。
ご興味があればぜひこれらの記事もご覧ください。
それではまたお会いできることを楽しみにしています。
【参考文献】
アクチュアリー試験、1次試験指定テキスト:二見隆著、生命保険数学<上巻>及び<下巻>
アクチュアリー試験、2次試験指定テキスト:保険1(生命保険)及び保険2(生命保険)







コメント