純保険料ってなに？ – 定義から計算方法までをわかりやすく解説

このページでは…

保険業界でアクチュアリーとして働いていた筆者が、生命保険の保険料の構成要素のひとつであり、解約返戻金の計算にも出てくる純保険料についてわかりやすく解説しています。

解約返戻金の計算方法を理解するうえで必要な考え方ですので、解約返戻金の計算方法についての記事を読む前に是非この記事をお読み頂ければと思います。

これまでのおさらい
～計算の準備～
純保険料の計算例①：保険期間１年の死亡定期保険
純保険料の計算例②：保険期間２年の死亡定期保険
純保険料の計算例③：保険期間10年の死亡定期保険
1. 死亡者数が一定の場合
2. 死亡率が一定の場合
（参考）保険期間が3年から9年の場合
まとめ
1. 【参考文献】

これまでのおさらい

純保険料の計算は、保険料の計算方法がしっかりわかっていれば早く理解することができます。保険料の計算方法については以下の記事でわかりやすく解説していますので、まだお読みになっていない方はこちらも是非読んでみてください。

～計算の準備～

まず始めに、タイトルにあるとおり純保険料とは何かについて解説します。

一般に、保険料は保険会社に集められた後に何に使われる予定なのかに応じて大きく２つの構成要素に分けることができます。この２つを専門用語で純保険料と付加保険料と呼びます。つまり常に以下の計算式が成り立ちます。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 純保険料 + 付加保険料 = 保険料 }} \end{align*} $$

上記のとおり保険料を使われ方によって分類しますので、純保険料を理解するには実際のお金の動きを想像するとわかりやすいです。保険料は保険会社に集められたあと、何に使われるのでしょうか？

保険料の構成要素①

まずは１つ目は主に保険金の支払に使われる部分です。ただここまで説明を簡単にしてしまうと実態が見えず計算式が立てられませんので、もう少しきちんと考えてみます。

保険を販売した時点で、保険会社は保険金を将来いつ払うことになるかは正確にはわかりません。亡くなったときに保険金を支払う商品であれば、１年目にお亡くなりになる方もいれば契約から数年間経った後にお亡くなりになる方もいるでしょう。支払われるタイミングは契約によって異なります。このため、保険会社はどれくらいの人が何年目に何人くらい亡くなるのかを過去の統計情報などを用いて予想します。これを専門用語で予定死亡率と呼びます。

また、１年目にお亡くなりになる人もいらっしゃるので、集めた保険料を全部運用に回してしまうと問題です。基本的には現金を一度運用に回してしまうと好きな時に好きな金額で現金に戻せるというわけではありません。保険金は当然現金で支払う必要がありますから、すぐに保険金として支払う可能性のある金額は現金として手元に残しておく必要があります。このため、保険会社は集めた保険料のうちいくらくらいを運用に回すのか、平均どれくらいの期間運用できるのかを考えます。そして最終的に平均何％で保険料を増やせるのかを予想します。これを専門用語で予定利率と呼びます。

つまり保険料の１つ目の構成要素についての正確な説明は、保険金の支払の予想金額に運用の利回りの予想を考慮して計算される金額ということになります。この部分が純保険料と呼ばれるものです。

保険料の構成要素②

次に２つ目は主に事業費に使われる部分です。保険料の構成要素のうち事業費に相当する部分を付加保険料と呼びます。本記事は純保険料について解説することが目的ですのでここでは割愛します。付加保険料については以下の記事で詳しく解説していますので、ご興味のある方はこちらも是非ご覧ください。

純保険料の計算の前提について

さて、文字だけで読むよりは具体的な計算例を見た方がわかりやすい場合もありますので、いつものとおり死亡保険の例で保険期間を１年、２年そして10年の例で順番に確認してみましょう。保険金額は100万円、利回り（予定利率）は年間５％とします。また、保険料の収入のタイミングは年始、保険金の支払のタイミングは年末とします。

また最後に死亡についてですが、死亡者数が年間２人の場合と死亡率が年間２%の場合（いずれも最初の人数は100人）の２つの例を考えてみます。なぜこの２つの例を考えるかについては深い理由がありますので、一旦このまま読み進めてみてください。

純保険料の計算例①：保険期間１年の死亡定期保険

まず保険期間１年の死亡定期保険の純保険料を求めてみます。最初の人数を100人とすると、計算式は以下のようになります。なお、最初の人数は死亡者数を人数としてイメージしやすいようにするためのもので、最終的な保険料の金額には影響しません。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ \underset{\scriptsize\mbox{純保険料収入}}{\underline{\mbox{保険料のうち保険金支払に使われる部分 × 100人}}} = \underset{\scriptsize\mbox{保険金支払}}{\underline{\mbox{100万円×2人} \div 1.05}} }} \end{align*} $$

保険料は年始に集めますので５％で運用できます。このため、年始で集めた保険料に1.05をかけた金額が保険金の支払いの期待値である２万円になる、と考えた方がわかりやすいかもしれません。この場合は右辺の1.05を左辺に移行した計算式になりますので、数学的には同じことです。ただ保険料の計算においては、常に契約時点に戻して考えます。このため、１年後に支払う保険金の契約時点の価値は２万円割る1.05で19,048円だから、契約時点で19,048円集めれば足りる、という考え方に慣れておくと良いでしょう。

計算結果を先に言ってしまいましたが、保険期間１年の死亡定期保険の純保険料は、上の計算式を計算して19,048円ということになります。

なお、この例では死亡者数が年間２人の場合と死亡率が年間２%の場合で死亡者数が変わりませんので、どちらも純保険料は19,048円になります。

純保険料の計算例②：保険期間２年の死亡定期保険

次に保険期間２年の死亡定期保険の例を考えてみましょう。

死亡者数が一定の場合

まず１つ目として毎年の死亡者数が２人の場合を考えます。毎年の死亡者が２人のため、保険料を集めることができる人数は、１年目は100人ですが、２年目は98人ということになります。これらに利回りを考慮して計算式を立てると以下のようになります。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ \underset{\scriptsize\mbox{１年目の純保険料収入}}{\underline{\mbox{純保険料}\times 100人}} + \underset{\scriptsize\mbox{２年目の純保険料収入}}{\underline{\mbox{純保険料}\times 98人 \div 1.05}} = \underset{\scriptsize\mbox{１年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05}} + \underset{\scriptsize\mbox{２年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05^2}} }} \end{align*} $$

この方程式を純保険料について解いてみます。純保険料は19,235円と求まりました。ここでとても重要なことは純保険料は保険料と同じで年によって変わらないことです。つまり純保険料は保険料のうち保険金の支払に充てられる平均的な金額を表していると言えます。また、保険期間１年の例よりも少し高くなりました。これはなぜでしょうか。答えは次の場合を確認してからの方がわかりやすいので、一旦次の例に移りましょう。

死亡率が一定の場合

２つ目として毎年の死亡率が２％の場合を考えます。最初の人数が100人のため、１年目の死亡者は２人、２年目の死亡者は1.96人ということになります。このため、保険料を集めることができる人数は、１年目は100人ですが、２年目は98人ということになります。これらに利回りを考慮して計算式を立てると以下のようになります。

この方程式を純保険料について解いてみます。面白いことに保険期間１年の例と同じ19,048円になりました。実は死亡率を一定とすると保険期間を延ばしても純保険料の金額は変わりません。これはなぜでしょうか。

死亡率が一定の場合の考察

いま計算した死亡率が一定の場合の方がわかりやすいため、先に金額が変わらなかった理由を考えてみます。

まず１年目ですが、100人の人から保険料を集めて２人に100万円を支払います。100人の人から19,048円集めて利回り５％で運用するので、年末には19,048円×100人×1.05 = 200万円となりぴったり年末の保険支払金額と一致します。

次に２年目ですが、98人の人から保険料を集めて1.96人に100万円を支払います。98人の人からそれぞれ19,048円集めて利回り５％で運用するので、年末には19,048円×100人×1.05 = 196万円となりぴったり年末の保険支払金額と一致します。

つまり死亡率が一定の場合、毎年集めた純保険料はその年のうちにすべて保険金として支払ってしまうということを意味しています。年始の人数に対し常に一定割合の死亡者が出るということの繰り返しのため、純保険料は保険期間が延びても変わらないという現象が起きるわけです。

死亡者数が一定の場合の考察

一方で保険期間が２年の例の１つ目の場合はどうでしょうか。１年目は100人の人から保険料を集めて２人に100万円を支払います。100人の人からそれぞれ19,235円を集めて利回り５％で運用するので、年末には19,235円×100人×1.05 = 2,019,704円となり200万円の保険金を支払って19,704円余ることになります。

２年目は98人の人から保険料を集めて２人に100万円を支払います。98人の人からそれぞれ19,235円を集めて利回り５％で運用するので、年末には19,235円×98人×1.05 = 1,979,310円となります。年末に支払う200万円の保険金に少し足りなそうです。

しかし実は１年目に余っていた19,704円もありますので、19,704円×1.05 = 20,690円も保険金の支払に充てられます。これを加えると200万円になります。期間を通算することでぴったり保険金の支払金額と一致することがわかります。

さて、ここで１年目はお金が余って２年目はお金が足りなかったことが重要です。これが死亡者数を一定とした場合に純保険料が保険期間１年の例よりも少し高くなる理由と関係しています。

答えは２年目の死亡者数が同じということは、２年目の死亡率が上昇していることを意味するためです。

今回で例では、１年目は100人の人数に対し２人死亡するため、死亡率は２％でした。一方で２年目は98人の人数に対し２人死亡することとなります。この場合の正確な死亡率は以下の計算で2.04%と求めることができます。

$$ \begin{align*} \color{black}{ \mbox{2.04% = 2人 ÷ 98人 × 100} } \end{align*} $$

つまりこれは、最初の人数が100人で死亡者数が毎年２人の場合、２年目以降の死亡率は２％より高くなるということです。死亡率が上昇すれば保険金の予想支払金額は当然増加しますので、純保険料も増加したわけです。

ここでは死亡者数が一定であることと死亡率が一定ということは同じではなく、死亡率が上昇することを意味することを押さえておきましょう。

純保険料の計算例③：保険期間10年の死亡定期保険

最後に保険期間が10年の場合を考えてみましょう。保険料の払込期間も同じ10年とします。

死亡者数が一定の場合

まずこれまでと同様に１つ目の場合として毎年の死亡者数が２人の場合を考えてみます。純保険料収入を求める計算式は以下のようになります。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料 = \underset{\scriptsize\mbox{１年目の純保険料収入}}{\underline{\mbox{保険料}\times 100人}} + \underset{\scriptsize\mbox{２年目の純保険料収入}}{\underline{\mbox{保険料}\times 98人\div 1.05}} + \underset{\scriptsize\mbox{３～８年目の純保険料収入}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{９年目の純保険料収入}}{\underline{\mbox{保険料}\times 84人\div 1.05^8}} + \underset{\scriptsize\mbox{10年目の純保険料収入}}{\underline{\mbox{保険料}\times 82人\div 1.05^9}} }} \end{align*} $$

毎年２人死亡するので年始の人数が100人、98人、96人、94人・・・というように減っていきます。このため、毎年集めることができる保険料も２人ずつ減っていきます。また、2年目以降の保険料については、集めるタイミングに応じて現在価値に直す必要があります。例えば10年目の保険料は10年目の年始に集めるため、契約時からちょうど9年間経ったタイミングで集めます。このため利回り５％では1.05で９回割って現在価値に調整しています。この計算式を経過年数をｔとおき、和の形で書き直すと以下のような形になります。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ \mbox{収入保険料} = \mbox{保険料} \times \sum_{t=0}^{9}\frac{100-2t}{1.05^t} }} \end{align*} $$

続いて、保険金支払について考えてみます。上記のとおり毎年の死亡者数が２人で一定のため、保険金の支払金額は毎年変わらず200万円です。但し、利回りの影響を考慮する必要がありますので、支払うタイミングに応じて1.05の階乗で割って現在価値に調整する必要があります。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 保険金支払 = \underset{\scriptsize\mbox{１年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05}} + \underset{\scriptsize\mbox{２年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05^2}} + \underset{\scriptsize\mbox{３～８年目の保険金支払}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{９年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05^9}} + \underset{\scriptsize\mbox{10年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05^{10}}} }} \end{align*} $$

純保険料収入の計算式と同様に経過年数をｔとおくことで、この計算式も和の形で表現することができます。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 支払保険金 = 100万円 \times 2人 \times \sum_{t=0}^{9}\frac{1}{1.05^{t+1}} }} \end{align*} $$

この計算式を保険料について解くと、保険料は20,749円と求めることができます。最初に求めた19,048円と比べて９%近く高くなりました。これは保険期間２年の例でも述べたとおり死亡率が上昇しているためです。例えば10年目ですと、年始の人数82人に対して２人死亡するため、2.44%(= 2 ÷ 82 × 100)となり、同じ２人の死亡者数でも死亡率はかなり上昇していることがわかります。

死亡率が一定の場合

次に２つ目の場合として毎年の死亡率が２％の場合を考えてみます。純保険料収入を求める計算式は以下のようになります。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料 = \underset{\scriptsize\mbox{１年目の純保険料収入}}{\underline{\mbox{保険料}\times 100人}} + \underset{\scriptsize\mbox{２年目の純保険料収入}}{\underline{\mbox{保険料}\times 98人\div 1.05}} + \underset{\scriptsize\mbox{３～８年目の純保険料収入}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{９年目の純保険料収入}}{\underline{\mbox{保険料}\times 85.05人\div 1.05^8}} + \underset{\scriptsize\mbox{10年目の純保険料収入}}{\underline{\mbox{保険料}\times 83.37人\div 1.05^9}} }} \end{align*} $$

生存者および死亡者の人数前回計算したとおりですので詳しい説明は割愛しますが、年始の人数が100人、98人、96.04人、94.12人・・・というように減っていきますので、毎年集めることができる保険料もその分減っていきます。また、２年目以降の保険料については、集めるタイミングに応じて現在価値に直す必要があります。例えば10年目の保険料は10年目の年始に集めるため、契約時からちょうど９年間経ったタイミングで集めます。このため利回り５％では1.05で９回割って現在価値に調整しています。この計算式を経過年数をｔとおき、和の形で書き直すと以下のような形になります。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 収入保険料 = \mbox{保険料} \times \sum_{t=0}^{9}\frac{\mbox{100×(1-2%)}^t}{1.05^t} }} \end{align*} $$

続いて、保険金支払について考えてみます。上記のとおり各年始の人数が年々減っていきますので、死亡率が一定であっても死亡者数は年々減っていきます。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 保険金支払 = \underset{\scriptsize\mbox{１年目の保険金支払}}{\underline{\mbox{100万円}\times 2人 \div 1.05}} + \underset{\scriptsize\mbox{２年目の保険金支払}}{\underline{\mbox{100万円}\times 1.96人 \div 1.05^2}} + \underset{\scriptsize\mbox{３～８年目の保険金支払}}{\underline{\mbox{・・・}}} + \underset{\scriptsize\mbox{９年目の保険金支払}}{\underline{\mbox{100万円}\times 1.70人 \div 1.05^9}} + \underset{\scriptsize\mbox{10年目の保険金支払}}{\underline{\mbox{100万円}\times 1.67人 \div 1.05^{10}}} }} \end{align*} $$

純保険料収入の計算式と同様に経過年数をｔとおくことで、この計算式も和の形で表現することができます。

$$ \begin{align*} \require{enclose} \enclose{roundedbox}[mathcolor=#ff9999] {\color{black}{ 支払保険金 = 100万円 \times \sum_{t=0}^{9}\frac{\mbox{100×(1-2%)}^t×\mbox{2%}}{1.05^{t+1}} }} \end{align*} $$

この計算式を保険料について解くと、保険料は19,048円と求めることができます。やはり最初の例と保険料が一致しました。この理由は保険期間２年目の例で解説したとおりです。

（参考）保険期間が3年から9年の場合

ご参考までに保険期間が１年から10年まで、上記の前提で純保険料を計算したものを表にしてみました。また参考として、エクセルなどでも簡単に再現できるかと思いますので、ご興味のある方は是非再計算してみてください！

	1	2	3	4	5	6	7	8	9	10
死亡者数一定の場合の純保険料	19,048	19,235	19,423	19,612	19,801	19,990	20,180	20,369	20,559	20,749
死亡率一定の場合の純保険料	19,048	19,048	19,048	19,048	19,048	19,048	19,048	19,048	19,048	19,048

表：保険期間と純保険料の関係（死亡者数一定の場合と死亡率一定の場合の比較）

また、同様に保険期間ごとにグラフにしてみました。差を強調するために18,000をY軸の下限としていますが、例えば10年目では９%程度の差しかありませんのでご注意ください。

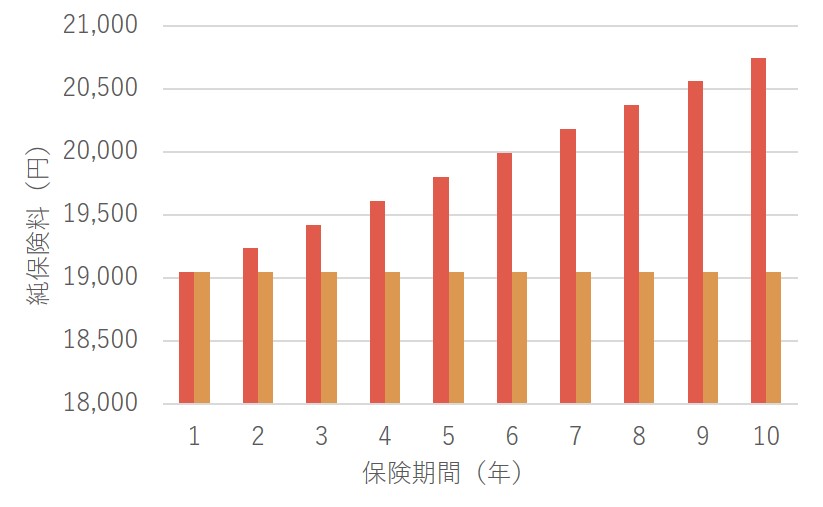
死亡者数一定の場合は死亡率の上昇に応じて比例的に純保険料が大きくなっている一方で、死亡率が一定の場合は純保険料は一定であることがわかります。このように純保険料は平均の死亡率を反映するということがおわかりいただけたかと思います。

まとめ

今回の記事では「純保険料ってなに？」と題して、死亡定期保険の純保険料について考え方と計算方法を解説していきました。純保険料は解約返戻金の計算のもとになる金額であるため、保険の契約者にとってとても重要なものです。この記事で純保険料について理解を深めた後は是非解約返戻金の計算方法についての記事もご覧ください。